Centre of gravity: It
is a defined as the point through which resultant
of force of gravity (weight) of the body
acts.
- C. G. of a Flat plate:
Centroid: If
the thickness of a solid body (say plate) reduces
to infinitesimal, then the plate reduces to
an area. Centroid is a point in a plane area such
that the moment of area about any axis
through
that point is zero.
Difference between centre of gravity and Centroid:
- The term centre of gravity applies to bodies with mass and weight, and centroid applies to plane area.
- Centre of gravity of a body is a. point through which the resultant gravitational force (weight) acts for any orientation ofthe body where as centroid is a point in a plane are such that the moment of area about any axis through that point is zero.
Eg:
- Centroid of a circle is its centre.
- Centroid of a rectangle of sides ‘b’ and ‘d’ is at a distance ‘b/2’ and ‘d/2’ from one corner.
Centroid of composite sections (Say I, T and L sections):
Step1:
Split the given composite section into suitable
standard figures and find the centroid of each of them.
Step
2: Assuming the area of simple figure as concentrated
at its centroid, its moment about
an
axis can be found by multiplying the area with
distance of its centroid from the reference axis.
Step
3: After determining the moment of each area
about reference axis, the distance of centroid
from the axis is obtained by dividing total
moment of area by total area of the composite
section.
Moment of Inertia:
Principal axes : Are defined as those about which
the product of Inertia is zero.
Principal
Moments of Inertia: Are the M . I for which
the product of inertia is zero.
The
maximum and minimum moments inertia
will be about the principal axes.
Where α = angle of major principal axis with horizontal
α1= α + 90 = angle of minor principal axis with horizontal
Note:
Ix + Iy =
i.e.,the
sum of moments of Inertia around two
mutually Perpendicular centroidal
axes is invariant(constant).
Parallel Axes Theorem: The
moment of inertia of a plane area with respect
to any axis in its plane is equal to the moment
of inertia with respect to a parallel centroid
axis plus the product of the total area and
the square of the distance between the two axes.
If
the moment of inertia of a plane area about an
axis through its e.g. is IGG , the moment of inertia
of the area about an axis AB parallel to the
first and at a distance ‘r’ from it, is given by
IAB = IGG +Ar2
Perpendicular Axes Theorem: (polar
moment of inertia) : If Ixx and Iyy be the moments
of inertia of a plane section about two mutually
perpendicular axes meeting at O, the moment
of inertia Izz, i.e., about an axis perpendicular
to both XX and YY passing
through
their point of intersection is given by
Izz
= lxx + Iyy
- Izz is called polar moment of inertia
- Solid circular section IZ = J = πd4/ 32
- Hollow circular section
- Square is IZ = a4/6
r
= (I/A)1/2
r
= Radius of gyration is in mm or cm.
- r for a solid circle is d/4
- r for a square is, a/2(3) 1/2
- Section modulus has units mm3 or cm3.


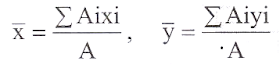








No comments:
Post a Comment