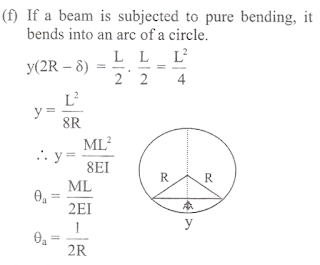
Relation between curvature, slope and deflection:
A = area of B.M.D.
Eg:
A simply supported beam of length L is subjected
to couples as shown in figure determine
maximum slope and deflection at the
centre of the beam?
- Double integration method:(Not suitable for objective type questions.)
- Area moment method:(for cantilevers, slopes and deflections can be determined very quickly.)
- Conjugate beam method:(very much suitable for beams of varying sections, subjected to couples, for cantilevers of S. S . Beams.)
- Macaulay ‘s method:(Also successive integration method.)
NOTE:
In double integration or Macaulay’s
method two constants of integration
C1 and C2 will be obtained. These
are determined using end conditions.
Mohr’s Theorem’s: Moment Area Method:
- Theorem 1: The angle between tangents drawn at any two points on the deflected curve, is equal to the area of M / El diagram between the two points.
A = area of B.M.D.
- Theorem 2: The intercept on a vertical line made by two tangents drawn at the two points on the deflected curve, is equal to the moment of M / EI diagram between the two points about the vertical line.
Ax̅ / EI x̅ = distance of C.G. of B.M.D.
E.G:
(Suitable for cantilevers)
Step
1 : To determine slope and deflection at any point.
Step
2 : Draw (BMD) / (EI)
i.e.,
M / EI
Step
3 : Slope = area of (M / EI) diagram between
fixed end point under consideration.
Step
4 : Deflection Ax̅ / EI
A
= B.M.D area between fixed end and point under consideration.
Ex.1
Consider
cantilever beam AB. Let ‘C’ be intermediate
point. Then the deflection at due
to a point load ‘P’ at B say YCB, is equal deflection
at ‘B’ due to a point load ‘P’ a









No comments:
Post a Comment