Highway Geometric Design (Transition Curves)

Transition Curves: (introduced between a straight and a circular curve).

(A) Objects of providing transition curves:

>> To introduce gradually the centrifugal force between the Tangent point and beginning of circular          curve, avoiding sudden jerk on the vehicle.

>> To enable the driver turn the steering gradually for comfort and security.

>> It introduces super elevation and extra widening on curves, gradually

>> To improve aesthetic appearance of road.

Transition curves have got radius of curvature gradually changing from infinity to the designed radius.

(B) Types of Transition Curves:

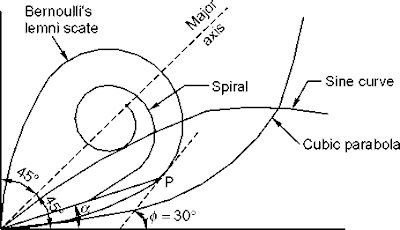
(i) Spiral (or Clothoid or Glover’s spiral):

>>This is the ‘Ideal transition curve’.

>> Radius of curvature at every point is inversely proportional to the distance of the point from the          beginning of the curve. 

>>Thus the rate of change of acceleration is uniform

>> L.R = Constant or 1 directly proportional to 1 / r

>> IRC recommends ‘Spiral’ as ideal transition curve

(ii) Bernoullie’s  Lemniscate :

>> Mostly used in modern roads where deflection angle n the curve is large

>> Radius of curve decreases more rapidly with the length

>> It is an auto genesis curve (follows a path which is actually traced by a vehicle when turning                freely)

>> The curve can be set by polar coordinates

(iii) Cubic parabola (Froude’s transition or easement curve)

>> Can be set by simple Cartesian coordinates

>> Used for valley curves

>> 

>> Condition is x=1; or cosφ =1

(iv) Cubic spiral:

>>simple to set the curve

>>

>>Condition is sinφ =φ = dy/dl

(c) Length of Transition Curves:

(i) Rate of change of radial (or centrifugal) acceleration:

v = Velocity in ‘m/see’

R = radius of curve in ‘m’

C = rate of change of centrifugal acceleration

(ii) Rate of change of Super elevation:

>> If pavement is rotated outer edge

L_s =  eN (W+W_w)

>> If pavement is rotated about centre line

L_S = eN ( W + We)/2

Where

W = normal width of pavement,

W_e = extra widening on circular curve

e= Super elevation

1 in N = Rate of change of super elevation.

As per IRC

>> N = 150 in plane and rolling trains

>> N = 60 in hill roads.

(iii) Empirical formulae (as per IRC):

For plain and rolling terrain,

L_s = 2.7V²/R

For mountainous or steep terrain, L_s =V² /R

The length of transition curve shall be the highest of the above.

Shift of the curve is s = L_s  ² = 24R